(1) 힙정렬
* 힙(heap)
최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(Complete binary tree)를 기본으로 한 자료구조
* 완전이진트리
노드를 삽입할 때 왼쪽부터 차례대로 추가하는 이진 트리

* 힙의 종류
부모노드의 키값이 자식노드의 키값보다 항상 큰 '최대 힙'
부모노드의 키값이 자식노드의 키값보다 항상 작은 '최소 힙'
* 완전이진트리 배열로 구현하기
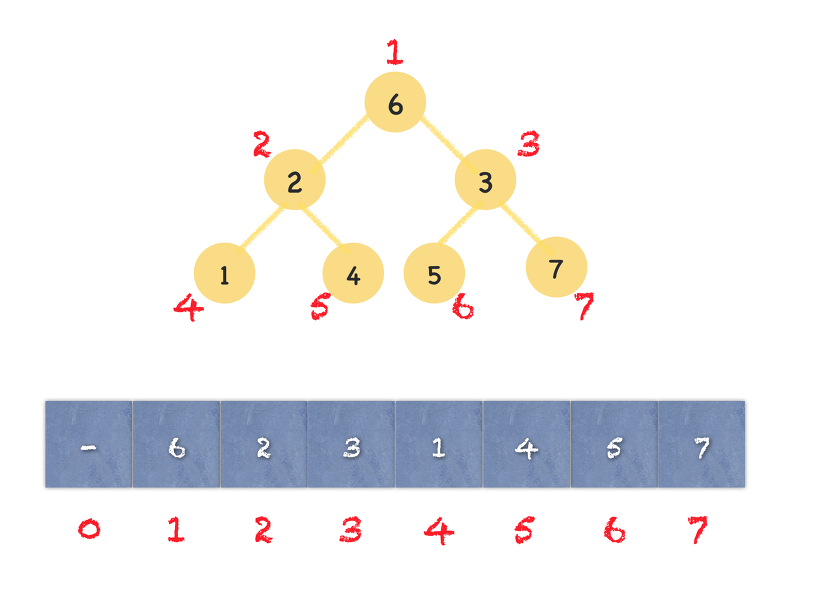
한 노드를 알면 그 노드의 부모, 자식들을 인덱스로 바로 접근 가능
노드 i의 부모 노드 인덱스 : i/2, (단, i > 1)
노드 i의 왼쪽 자식 노드 인덱스 : 2 x i
노드 i의 오른쪽 자식 노드 인덱스 : (2 x i) + 1
* 최대힙에서 힙 정렬하기
최대힙 직계관계에서는 무조건 부모는 자식(해당 노드)보다 키 값이 커야한다.

정렬되어있지 않은 배열이 주어졌을 때, 이를 완전이진트리로 만들면 위와 같음
이를 최대힙으로 만들기 위해서는 왼쪽 밑부터 검사를 시작해야 한다.

이 7은 15, 14와 2번의 비교과정을 거치게 된다. 그 중 큰값과 자리를 바꾸며, 만약 7이 두 자식보다 크다면 자리를 유지한다.
그 옆 부분트리로 넘어가자.

부모인 9가 최대값이 아니므로 위와 같이 12, 10과 비교하고 큰 값과 자리를 바꿔준다.
최대힙을 만드는 과정은 재귀로 이루어지기 때문에, [11, 8, 6]으로 이루어진 부분 트리를 검사하는 것 아님.
아래와 같이 부모노드가 3인 부분트리를 검사한다.
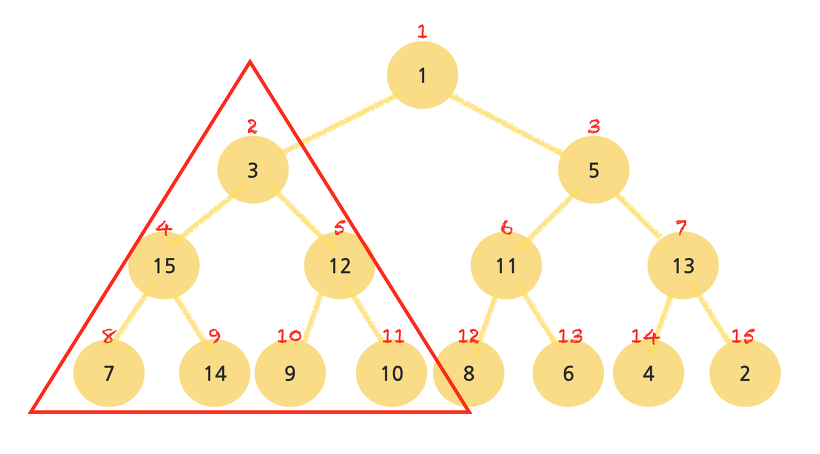
3이 15, 12보다 작으므로 이를 비교하고, 가장 큰 값과 자리를 바꾼다.

하지만 바꾼 후 [3, 7, 4] 부분노드의 부모노드가 자식노드보다 작으므로 7, 14와 비교하고 더 큰값과 자리를 바꾼다.
왼쪽 부분노드의 정렬이 끝났으면, 다음엔 오른쪽 부분노드!

오른쪽 부분노드의 정렬도 끝났으면, 전체 트리를 검사해야 한다.
하지만 여기에서도 순서조건이 만족하지 않음.



1이 내려가야 한다. 14, 12중 더 큰 수와 자리를 바꾼다. 하지만 1이 밑으로 내려감으로써 아래 트리의 순서가 맞지 않게 됨.
다시 바꾼다. 7, 3중에 더 큰 값과 1의 자리를 바꿈.
이제 모든 트리가 순서조건을 만족하게 되었다.
완성 후 배열은 아래와 같다.

여기까지 최대힙을 만드는 과정(Heapify)이었음.
이렇게 배열이 정렬 된후에는 오름차순의 출력을 위해 다시 한번 정렬해주어야함.
루트노드에는 최대값이 담겨있는데, 이를 삭제하는 방법을 통해 정렬을 진행한다. => 힙의 삭제 연산!

배열의 마지막 값과, 첫번째 값의 위치를 바꾸어준다. 힙에서 최대값인 15는 사라진 것임(삭제)
따라서, 배열의 크기를 하나 줄인다. (실제로 배열의 크기를 줄이는 것이 아닌 마지막 index를 빼고 연산하는 것)
위치를 바꾸고 마지막 index를 줄인 트리에서 다시 최대힙을 만드는 과정을 수행함.
-> 최대값이 루트노드에 담기게 된다. -> 이 루트노드를 배열의 마지막 값과 바꿈 -> 다시 최대힙을 만든다(Heapify 수행)
이 과정을 반복!
(2) 병합정렬
[4, 2, 6, 3, 7, 8, 5, 1]
[4, 2, 6, 3] [7, 8, 5, 1] 2개로 나눈 후 또 [4, 2] [6, 3] [7, 8] [5, 1]로 자른다.
[4][2] / [6][3] / [7][8] / [5][1]로 각각 나누어 2개씩 비교하며 정렬한다.
정렬된 배열을 다른 배열과 비교한다. 정렬을 통해 작은 수를 앞에 두었으므로 앞에있는 수(ex. 2와 3) 끼리만 비교하면 된다.
[2, 4]
[3, 6]을 비교한다. 2는 3보다 작다. [2]
[4]
[3, 6] 3은 4보다 작다. [2, 3]
[4]
[6] 4는 6보다 작다. [2, 3, 4]
결과적으로 [2, 3, 4, 6]이 된다.
[7, 8] [1, 5]도 똑같이 비교하면 [1, 5, 7, 8]이 됨.
그 후에 정렬된 배열 2개 [2, 3, 4, 6] [1, 5, 7, 8]을 위와 같은 방법으로 비교하면 오름차순으로 정렬된 배열이 완성된다.
정리하자면 아래와 같다.
1. 리스트 길이가 1이 될때까지 반으로 나눈다. 분할(Divide)
2. 다 나누어 졌다면, 데이터를 정렬하며 다시 합친다. (Merge)
즉, 함수가 호출 될 때마다 절반씩 잘라 재귀적으로 호출하고, 작은 배열부터 2개씩 비교해 병합하면서 최종적인 배열을 만드는 정렬 방법이다.
BUT, 병합 정렬은 별도의 저장 공간을 필요로 한다. 하나의 배열이 더 필요함!


(3) 퀵정렬
분할 정복 알고리즘
특정한 값(기준값, 피벗)을 기준으로 큰 숫자와 작은숫자를 서로 교환한 뒤에 배열을 반으로 나누어 진행한다. (피벗은 가장 앞에있는 숫자로 설정)
1. 피벗을 정한 뒤 왼쪽애서 오른쪽으로, 오른쪽에서 왼쪽으로 이동하며 검사 (피벗은 중간 값으로 잡는다.)
2. 왼쪽에서 오른쪽으로 이동할 는 피벗보다 큰 값을, 오른쪽에서 왼쪽으로 이동할 때는 작은 값을 선택
3. 두 개의 값이 선택이 완료되었다면 두 값을 swap
4. 계속해서 왼쪽->오른쪽, 오른쪽->왼쪽으로 이동하며 값을 찾고 swap (반복)
5. 값이 엇갈리는 경우에는 이동을 멈춘다 (작은 값의 index가 큰 값의 index보다 작아지는 경우)
6. 그리고 피벗 값과 작은 값(오른쪽 -> 왼쪽 이동하며 선택한 값)을 바꿔준다. => 이때 피벗값은 정렬이 완료되었다 할 수 있음
* 피벗값이었던 수를 기준으로 왼쪽은 모두 피벗값보다 작고, 오른쪽은 모두 크기 때문!
7. 피벗값이었던 수를 기준으로 왼쪽과 오른쪽이 분할되었다. 이후 분할된 왼쪽과 오른쪽 배열에서 다시 피벗값을 찾고 정렬을 진행해주면 됨 (반복)


'CS > Algorithm' 카테고리의 다른 글
| [Algorithm] 동적 계획법(Dynamic Programming, DP) (0) | 2019.08.31 |
|---|---|
| [Algorithm] 카운팅(계수) 정렬 개념 (0) | 2019.08.31 |
| [Algorithm] 순환(Recursion) (0) | 2019.06.09 |
| [Algorithm] 알고리즘의 분석 (0) | 2019.06.03 |
| [Java] 문자열 관련 함수 (0) | 2019.04.16 |